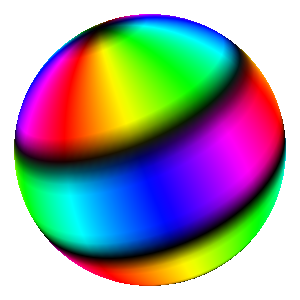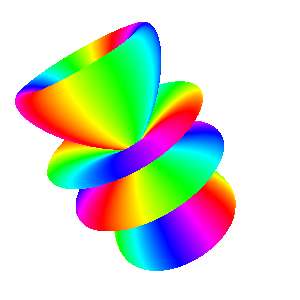|
|
This applet provides a 3D representation of spherical harmonics \(Y_{\ell,m}(\theta,\varphi)\) as a function of spherical coordinates \(\theta\) and \(\varphi\), for specified values of \(\ell\) and \(m\). The mouse can be used to change the point of view and the zooming factor.
Three plot types are available, as shown in the example below for \(Y_{5,2}(\theta,\varphi)\).
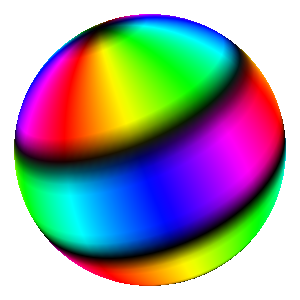
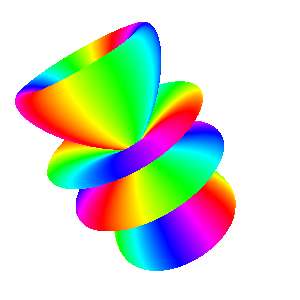

- In the "Sphere" mode (left), the complex function is directly plotted on a sphere, the absolute value
being encoded on the brightness and the argument (phase) on the color.
- In the "Complex surface" mode (center), the distance of the plotted surface from the origin is equal to the absolute
value of \(Y_{\ell,m}(\theta,\varphi)\), while the phase is again color encoded.
- In the "Real surface" mode (right), an alternate basis is used where \(Y_{\ell,|m|}(\theta,\varphi)\) and \(Y_{\ell,-|m|}(\theta,\varphi)\)
are replaced with the two real functions \({\rm Re}\,Y_{\ell,|m|}(\theta,\varphi)\) and \({\rm Im}\,Y_{\ell,|m|}(\theta,\varphi)\), spanning the same 2D vectorial space.
The color then encodes the sign, with cyan for positive values and red for negative values. Note that, in this case, these real functions are no longer eigenfunctions of \(\hat L_z\).
By convention, positive (resp. negative) \(m\) values on the dropdown box allow to plot the real (resp. imaginary) part of \(Y_{\ell,|m|}(\theta,\varphi)\).
Finally, you can adjust the number of segments used to compute the surface along meridians and parallels. A greater number of segments provides a higher-quality surface but with
a slower update rate.
Background
Spherical harmonics \(Y_{\ell,m}(\theta,\varphi)\) are the common eigenvectors of the two commuting observables \(\hat L^2\) and \(\hat L_z\), where \(\hat {\vec L}\) is the angular momentum operator. We thus have
\[
\hat L^2 Y_{\ell,m}(\theta,\varphi) = \ell(\ell+1)\hbar^2 Y_{\ell,m}(\theta,\varphi)\qquad\qquad\mbox{and}\qquad\qquad\hat L_z Y_{\ell,m}(\theta,\varphi) = m \hbar Y_{\ell,m}(\theta,\varphi),
\]
where \(\ell\in \mathbb{N}\) and \(m\) is an integer such that \(|m|\le\ell\). In spherical coordinates, these two operators read
\[
\hat L^2 = -\hbar^2\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta} \sin\theta\frac{\partial}{\partial \theta} + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial\varphi^2}\right)\qquad\qquad\mbox{and}\qquad\qquad\hat L_z = \frac{\hbar}{i} \frac{\partial}{\partial \varphi},
\]
so that common eigenfunctions read
\[
Y_{\ell,m}(\theta,\varphi) = F_{\ell,m}(\theta) \exp(im\varphi).
\]
It can be shown that the real function \( F_{\ell,m}(\theta)\) has exactly \(\ell-|m|\) nodes in the interval \(]0,\pi[\), as can be checked using the above applet.
Also evident in the representation is the wrapping of \(|m|\) period along a parallel when \(\varphi\) varies from \(0\) to \(2\pi\), due to the \(m\varphi\) phase factor.
|